Légvédelemi radarok működéséről általában

Törölt tag · 2019. március 1.

Terminator said:
Akkor milyen messziről nem látta az F-35-öst?

Jah, azt hittem hogy már mindenkinek megy magától is...
:rolleyes:

Kezdjük az antenna nyereségének megbecslésével.
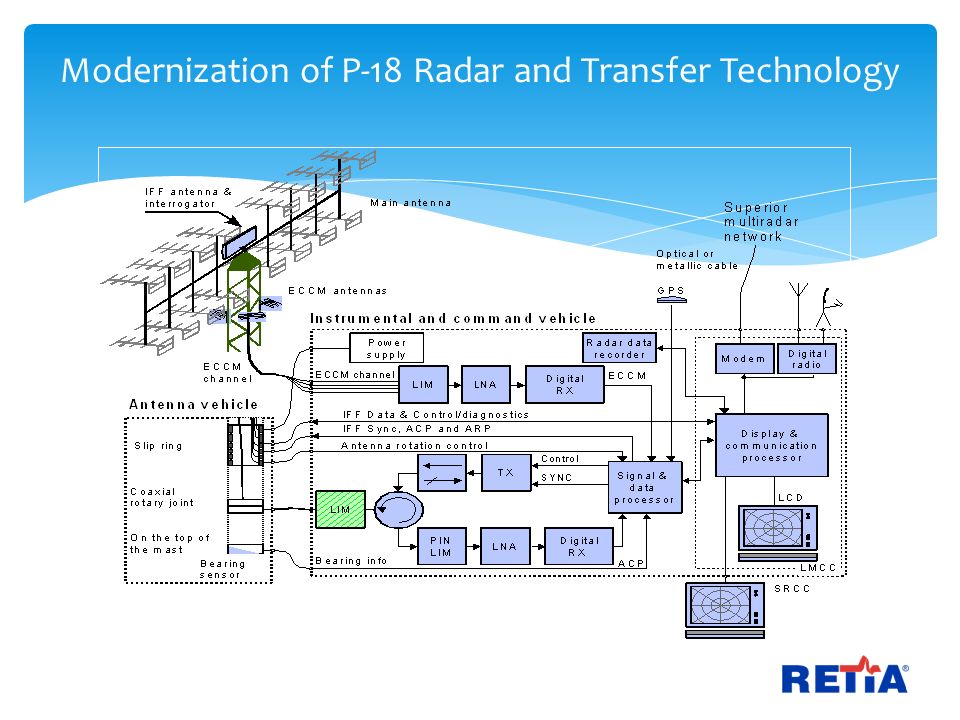
Ez egy 6x16db vízszintes Yagi dipól antennából álló rács.

Mivel nem ismerjük az általa kibocsájtott nyaláb paramétereit, egy alap Yagi antennából indulunk ki, ami helyszögben 90°, oldalszögben 50°-os nyalábot állít elő.
Látható a képen, hogy itt az antennák vízszintesen polarizáltak.

nyaláb átmérője helyszögben (6db antenna függőlegesen)
o1 = 90° / 6db = 15°

nyaláb átmérője oldalszögben (16db antenna vízszintesen)
o2 = 50° / 16db = 3.125°

RadarTutorial oldalról veszem a távolsági felbontást (600m) amiből számolunk egy vételi érzékenységet.
PR = -96dB + 10*log(300/600m) = -99dBm

Számítsuk ki az antenna nyereséget, 15° x 3.125° fokos nyaláb esetére.
o1, o2 - nyalábátmérő
2xG= 20*log(29000/((o1 * o2)) = 20*log(29000/((15° * 3.125°)) = 55.8dBi

Hasonló adókkal (20kW) számolok mint a NEBO-M esetén, 6dbx16db = 96db elemre.
96db x 20kW = 1.92MW
PT = 10 * log (1'920'000'000mW) = 92.8dBm

Kiszámítom a terjedési veszteséget, mondjuk 300MHz frekvenciát feltételezve.
20 log(F) = 20 log (300MHz) = 49.5dB

Namost feltételezzük hogy az F-35-ös radar-keresztmetszete mondjuk -29dBsm.
40 log(D) = PT - PR + 2G - 103 - 20 log(F) + 10 log(o)
40 log(D) = 92.8dBm - -99dBm + 55.8dBi - 103 - 49.5dB - 29dBsm = 66.1dB
log(D) = 1.6525
D = 10^1.6525 = 45km <- ennyi lenne tehát az általunk becsült JY-27 felderítési távolsága egy -29dB
radar-keresztmetszetű cél esetén.
:cool:

gacsat · 2019. március 1.

Terminator said:
Akkor milyen messziről nem látta az F-35-öst?

Azt gondolom, 90 km-ről.

ghostrider · 2019. március 3.

Még ha látta is, vajon mit tudtak volna csinálni? Nem tudjuk, hogy mit és mennyit indítottak rá.

Pocok75 · 2019. március 3.

Az ok hogy látja, de mi világítja meg a célt a léraknak, mert úgy tudom ezek azt nem tudnak, vagy tévedek?

zsolti · 2019. március 3.

Pocok75 said:
Az ok hogy látja, de mi világítja meg a célt a léraknak, mert úgy tudom ezek azt nem tudnak, vagy tévedek?

Nem, nem tévedsz, ez nem arra van, hanem csak annyi a cél, hogy egyáltalán legyen fogalma az üzemeltetőnek hogy kb. merre és milyen távolságon van ellenséges stealth jármű. No meg ha meg is tudná világítani a célt(nem tudja), akkor is ehhez nem ártana valami IRIS-T SL szintű rakéta.

Pocok75 · 2019. március 3.

Arra van lehetőség, hogy a célt meg mutatja kb merre van és a lérak radarja, szűkítet nyalábbal esetleg megláthatja? Vagy erre nincs lehetőség? Hogy arányul a felderítési távolság? Pl, ha ez a felderítő radar 45kmről látja a célt, akkor a tűzvezető lokátornak milyen távolságból van esélye befogni a célt? Bocsi, de totál analfabéta vagyok a témához. :rolleyes:

molnibalage · 2019. március 3.

Pocok75 said:
Arra van lehetőség, hogy a célt meg mutatja kb merre van és a lérak radarja, szűkítet nyalábbal esetleg megláthatja? Vagy erre nincs lehetőség? Hogy arányul a felderítési távolság? Pl, ha ez a felderítő radar 45kmről látja a célt, akkor a tűzvezető lokátornak milyen távolságból van esélye befogni a célt? Bocsi, de totál analfabéta vagyok a témához.

A HTÖ erre vonatkozólag is mutat be eszmefuttatást az Sz-300/400 családra vonatkozólag. A Nyebo szóra keress rá benne. A Nyebohóz képest a tűzvezető radar jó, ha fele távolságról képes észlelni a -30 dBsm méretű célt.

Törölt tag · 2019. március 3.

Pocok75 said:
Arra van lehetőség, hogy a célt meg mutatja kb merre van és a lérak radarja, szűkítet nyalábbal esetleg megláthatja? Vagy erre nincs lehetőség? Hogy arányul a felderítési távolság? Pl, ha ez a felderítő radar 45kmről látja a célt, akkor a tűzvezető lokátornak milyen távolságból van esélye befogni a célt? Bocsi, de totál analfabéta vagyok a témához.

Jók a kérdések!

Az Sz-400 komplexum 92N6E MFR [Grave Stone] tűzvezető lokátora 250km távolságból észlel egy 4m² radar-keresztmetszetű célt, a lenti reklámanyag szerint.

Számoljuk ki, hogy mekkora távolságból képes észlelni egy -29dBsm radar-keresztmetszetű célt?

Radar egyenlet: 40 log(D) = PT - PR + 2G - 103 - 20 log(F) + 10 log(o)
A fentiből csak a D - távolság, és az o - radar-keresztmetszet érdekel, a többi tagot összevonom x-re.

40 log(D) = x + 10 log(o)

Kiszámolom x-et, a 92N6E MFR [Grave Stone] tűzvezető lokátorra.

40 log(D) - 10 log(o) = x
x = 40 log (250km) - 10 log (4m²) = 89.9dB

Máris megvan az egyszerűsített radaregyenlet, a 92N6E MFR [Grave Stone] tűzvezető lokátorra.

40 log(D) = x + 10 log(o) = 89.9dB + 10 log (o)

92N6E MFR [Grave Stone] tűzvezető lokátor felderítési távolsága (F-35A becslésem szerint) o=-29dBsm célra
40 log(D) = 89.9dB + 10 log (o)
40 log(D) = 89.9dB - 29dBsm
40 log(D) = 60.9dB
log(D) = 1.5225
D = 10^1.9825 = 33km

Pocok75 · 2019. március 3.

molnibalage said:
A HTÖ erre vonatkozólag is mutat be eszmefuttatást az Sz-300/400 családra vonatkozólag. A Nyebo szóra keress rá benne. A Nyebohóz képest a tűzvezető radar jó, ha fele távolságról képes észlelni a -30 dBsm méretű célt.

@molnibalage Megvallom az őszintét, még a felét sem sikerült elolvasnom! :oops:

Áprilisban a család 2 hétre haza utazik, akkor lesz kis időm befejezni! Promise!

Pocok75 · 2019. március 3.

Hpasp said:
Jók a kérdések!

Az Sz-400 komplexum 92N6E MFR [Grave Stone] tűzvezető lokátora 250km távolságból észlel egy 4m² radar-keresztmetszetű célt, a lenti reklámanyag szerint.

Számoljuk ki, hogy mekkora távolságból képes észlelni egy -29dBsm radar-keresztmetszetű célt?

Radar egyenlet: 40 log(D) = PT - PR + 2G - 103 - 20 log(F) + 10 log(o)
A fentiből csak a D - távolság, és az o - radar-keresztmetszet érdekel, a többi tagot összevonom x-re.

40 log(D) = x + 10 log(o)

Kiszámolom x-et, a 92N6E MFR [Grave Stone] tűzvezető lokátorra.

40 log(D) - 10 log(o) = x
x = 40 log (250km) - 10 log (4m²) = 89.9dB

Máris megvan az egyszerűsített radaregyenlet, a 92N6E MFR [Grave Stone] tűzvezető lokátorra.

40 log(D) = x + 10 log(o) = 89.9dB + 10 log (o)

92N6E MFR [Grave Stone] tűzvezető lokátor felderítési távolsága (F-35A becslésem szerint) o=-29dBsm célra
40 log(D) = 89.9dB + 10 log (o)
40 log(D) = 89.9dB - 29dBsm
40 log(D) = 60.9dB
log(D) = 1.5225
D = 10^1.9825 = 33km

Szóval akkor a SDB II simán elég, bármilyen célpont ellen? Milyen esély van felderíteni egy ekkor célt, főleg aktív zavarásban?

Törölt tag · 2019. március 7.

Civil telekom cégek pont most készülnek az 5G bevezetésével AESA antennákkal teleszórni a világot.

https://networks.nokia.com/solutions/massive-mimo

angelsoul · 2019. március 7.

Hpasp said:
Civil telekom cégek pont most készülnek az 5G bevezetésével AESA antennákkal teleszórni a világot.

https://networks.nokia.com/solutions/massive-mimo

Egyik haverom ezek telepítésén dolgozik, bár én nem értek hozzá, annyit levágtam, hogy szerinte ezek állati veszélyesek az egészségre és konkrétan ő sem tudja, ez hogy lesz megoldva az üzemük.

Törölt tag · 2019. március 7.

angelsoul said:
Egyik haverom ezek telepítésén dolgozik, bár én nem értek hozzá, annyit levágtam, hogy szerinte ezek állati veszélyesek az egészségre és konkrétan ő sem tudja, ez hogy lesz megoldva az üzemük.

Az agyunkat már úgyis szétsugározta a 3G mobilinternet...
2007-es index cikk

gacsat · 2019. március 7.

Hpasp said:
Civil telekom cégek pont most készülnek az 5G bevezetésével AESA antennákkal teleszórni a világot.

https://networks.nokia.com/solutions/massive-mimo

Mi az az 5G?

gacsat · 2019. március 7.

Hpasp said:
Az agyunkat már úgyis szétsugározta a 3G mobilinternet...
2007-es index cikk

Hát az övéket valami biztos.

Törölt tag · 2019. március 20.

Urak!

Találós kérdés...
...ha egy lokátor egy 20 m2-es visszaverő felületű célt 400 km-ről érzékel, akkor egy F-35-öst (legyen mondjuk -29dBsm) mekkora távolságból tudja észlelni?

megoldás menete erre...

Törölt tag · 2019. március 21.

Hpasp said:
Urak!

Találós kérdés...
...ha egy lokátor egy 20 m2-es visszaverő felületű célt 400 km-ről érzékel, akkor egy F-35-öst (legyen mondjuk -29dBsm) mekkora távolságból tudja észlelni?

Találós kérdés...
...ha egy lokátor egy 20 m2-es visszaverő felületű célt 400 km-ről érzékel, akkor egy F-35-öst (legyen mondjuk -29dBsm) mekkora távolságból tudja észlelni?

Számoljuk ki, hogy mekkora távolságból képes észlelni egy -29dBsm radar-keresztmetszetű célt?

Radar egyenlet: 40 log(D) = PT - PR + 2G - 103 - 20 log(F) + 10 log(o)
A fentiből csak a D - távolság, és az o - radar-keresztmetszet érdekel, a többi tagot összevonom x-re.

40 log(D) = x + 10 log(o)

Kiszámolom x-et...

40 log(D) - 10 log(o) = x
x = 40 log (400km) - 10 log (20m²) = 91dB

Máris megvan az egyszerűsített radaregyenlet...

40 log(D) = x + 10 log(o) = 91dB + 10 log (o)

A kérdéses lokátor felderítési távolsága (F-35A becslésem szerint) -29dBsm célra
40 log(D) = 91dB + 10 log (o)
40 log(D) = 91dB - 29dBsm = 62dB
40 log(D) = 62dB
log(D) = 62dB / 40 = 1.55
D = 10^1.55 = 35km

ghostrider · 2019. április 28.

R-416GM (Р-416ГМ) cm-es rádió átjátszó (relé) állomás

R-419L1 (Р-419Л1) dm-es rádió átjátszó (relé) állomás

ghostrider · 2019. április 28.

3D(imenziós) 48Ja6-K1 Podlet-K1 (48Я6-К1 Подлет-К1) mobil felderítő lokátor állomás (pk-i és antenna hordozó jármű)

ghostrider · 2019. április 28.

Az alap 2D P-18M (П-18M) VHF sávú felderítő-célkövető lokátor állomás Parol saját-ellenség felismerő rendszerrel telepítve Oo.-ban

P-18_radar_at_the_Khotilovo_Air_Force_base_near_Tver.jpg

Szíriában, kicsit leharcolt állapotban

Mo.-on süllyesztett fedezékben, a régebbi NRZ saját-ellenség felismerő rendszerrel

a modernizált digitális változatok
1. P-18R belső digitális modernizáció

2. P-18-2 (П-18-2).

Az antenna rendszer kicsit mobilabb lett.

Légvédelemi radarok működéséről általában

Törölt tag

Guest

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

molnibalage

Guest

Törölt tag

Guest

Well-Known Member

Well-Known Member

Törölt tag

Guest

Well-Known Member

Törölt tag

Guest

Well-Known Member

Well-Known Member

Törölt tag

Guest

Törölt tag

Guest

Well-Known Member

Well-Known Member

Well-Known Member

Sütibeállításokkal kapcsolatos információk