Sz-75 Dvina / S-75 Dvina / SA-2 Guidline (Szovjetunió)
- Téma indítója Tcat
- Indítva
-
Ha nem vagy kibékülve az alapértelmezettnek beállított sötét sablonnal, akkor a korábbi ígéretnek megfelelően bármikor átválthatsz a korábbi világos színekkel dolgozó kinézetre.
Ehhez görgess a lap aljára és a baloldalon keresd a HTKA Dark feliratú gombot. Kattints rá, majd a megnyíló ablakban válaszd a HTKA Light lehetőséget. Választásod a böngésződ elmenti cookie-ba, így amikor legközelebb érkezel ezt a műveletsort nem kell megismételned. -
Az elmúlt időszak tapasztalatai alapján házirendet kapott a topic.
Ezen témában - a fórumon rendhagyó módon - az oldal üzemeltetője saját álláspontja, meggyőződése alapján nem enged bizonyos véleményeket, mivel meglátása szerint az káros a járványhelyzet enyhítését célzó törekvésekre.
Kérünk, hogy a vírus veszélyességét kétségbe vonó, oltásellenes véleményed más platformon fejtsd ki. Nálunk ennek nincs helye. Az ilyen hozzászólásokért 1 alkalommal figyelmeztetés jár, majd folytatása esetén a témáról letiltás. Arra is kérünk, hogy a fórum más témáiba ne vigyétek át, mert azért viszont már a fórum egészéről letiltás járhat hosszabb-rövidebb időre.
-
Az elmúlt időszak tapasztalatai alapján frissített házirendet kapott a topic.
--- VÁLTOZÁS A MODERÁLÁSBAN ---
A források, hírek preferáltak. Azoknak, akik veszik a fáradságot és összegyűjtik ezeket a főként harcokkal, a háború jelenlegi állásával és haditechnika szempontjából érdekes híreket, (mindegy milyen oldali) forrásokkal alátámasztják és bonuszként legalább a címet egy google fordítóba berakják, azoknak ismételten köszönjük az áldozatos munkáját és további kitartást kívánunk nekik!
Ami nem a topik témájába vág vagy akár csak erősebb hangnemben is kerül megfogalmazásra, az valamilyen formában szankcionálva lesz
Minden olyan hozzászólásért ami nem hír, vagy szorosan a konfliktushoz kapcsolódó vélemény / elemzés azért instant 3 nap topic letiltás jár. Aki pedig ezzel trükközne és folytatná másik topicban annak 2 hónap fórum ban a jussa.
T
Törölt tag 1945
Guest
No akkor fordítsuk komolyra a szót, és lássuk mennyire lehet egy adott analóg radar képességét számítással modellezni/előrejelezni.
Számoljunk egy SzA-75M Dvina tűzvezető lokátor átlagos MiG-21 felderítési távolságát.
Első lépés a hőzaj kiszámítása: kTB
Boltzmann állandó: k=1.38*10^-23 joule/K°
Üzemi hőmérséklet: T=290K° (17C°)
10 * log (kTB) = 10 * log (1.38 * 10^-23 joule/K° * 290K° * 1MHz) = 10 * log (4*10^-15) = -144dBW = -114dBm
Itt saccolunk egyet
tipikus zaj: 5dB
tipikus jel zaj viszony: 13dB
összesen tehát a hőzaj: -114dBm + 5dB + 13dB = -96dBm ami 1MHz sávszélességre érvényes, 17C° hőmérsékleten.
A Dvina komplexum V-750V légvédelmi rakétájának 196kg-os harci része 60m-en belül garantáltan hatásos, így ebből a komplexum számára szükséges távolság mérés pontosságára 120m adódik.
Tudjuk hogy 120m-t a fény 0.4μs alatt tesz meg, így a vevő szükséges sávszélessége kiszámolható:
B = 1/0.4μs = 2.5Mhz
Ebből már lehet becsülni egy átlagos vevőérzékenységet:
PR = -96dB + 10*log(2.5) = -92dBm
A Dvina tűzvezető lokátora 10° x 2° fokos legyezőnyalábot állít elő.
Számítsuk ki az antenna nyereséget.
o1, o2 - nyalábátmérő
G= 10*log(29000/((o1 * o2)) = 10*log(29000/((10° * 2°)) = 31.6dBi
A Dvina adó csúcsteljesítménye; 600kW = 600'000'000mW
PT = 10 * log (600'000'000mW) = 87.8dBm
És akkor jöhet az általános radaregyenlet:
PR = PT + 2G - 103 - 40 log(D) - 20 log(F) + 10 log(o)
ahol
PR - vételi teljesítmény (érzékenység); -92dBm
PT - adóteljesítmény; 87.8dBm
G - antenna nyereség; 31.6dBi
D - felderítési távolság; ezt keressük
F - frekvencia; 3GHz = 3000MHz
o - MiG-21 cél radarkeresztmetszete; 2m²
Az átlagos felderítési távolságra vagyok kíváncsi, az egyenletet átrendezem:
40 log(D) = PT - PR + 2G - 103 - 20 log(F) + 10 log(o)
40 log(D) = 87.8dBm - -92dBm + 2* 31.6dBi - 103 - 20 log (3000MHz) + 10 log(2sqrm)
40 log(D) = 87.8dBm + 92dBm +63.2dBi - 103 - 69.5dB + 3dBsm = 73.5dB
40 log(D) = 73.5dB
log(D) = 1.8375
D = 10^1.8375 = 69km <- ez bizony reális, örülünk.
Számoljunk egy SzA-75M Dvina tűzvezető lokátor átlagos MiG-21 felderítési távolságát.
Első lépés a hőzaj kiszámítása: kTB
Boltzmann állandó: k=1.38*10^-23 joule/K°
Üzemi hőmérséklet: T=290K° (17C°)
10 * log (kTB) = 10 * log (1.38 * 10^-23 joule/K° * 290K° * 1MHz) = 10 * log (4*10^-15) = -144dBW = -114dBm
Itt saccolunk egyet
tipikus zaj: 5dB
tipikus jel zaj viszony: 13dB
összesen tehát a hőzaj: -114dBm + 5dB + 13dB = -96dBm ami 1MHz sávszélességre érvényes, 17C° hőmérsékleten.
A Dvina komplexum V-750V légvédelmi rakétájának 196kg-os harci része 60m-en belül garantáltan hatásos, így ebből a komplexum számára szükséges távolság mérés pontosságára 120m adódik.
Tudjuk hogy 120m-t a fény 0.4μs alatt tesz meg, így a vevő szükséges sávszélessége kiszámolható:
B = 1/0.4μs = 2.5Mhz
Ebből már lehet becsülni egy átlagos vevőérzékenységet:
PR = -96dB + 10*log(2.5) = -92dBm
A Dvina tűzvezető lokátora 10° x 2° fokos legyezőnyalábot állít elő.
Számítsuk ki az antenna nyereséget.
o1, o2 - nyalábátmérő
G= 10*log(29000/((o1 * o2)) = 10*log(29000/((10° * 2°)) = 31.6dBi
A Dvina adó csúcsteljesítménye; 600kW = 600'000'000mW
PT = 10 * log (600'000'000mW) = 87.8dBm
És akkor jöhet az általános radaregyenlet:
PR = PT + 2G - 103 - 40 log(D) - 20 log(F) + 10 log(o)
ahol
PR - vételi teljesítmény (érzékenység); -92dBm
PT - adóteljesítmény; 87.8dBm
G - antenna nyereség; 31.6dBi
D - felderítési távolság; ezt keressük
F - frekvencia; 3GHz = 3000MHz
o - MiG-21 cél radarkeresztmetszete; 2m²
Az átlagos felderítési távolságra vagyok kíváncsi, az egyenletet átrendezem:
40 log(D) = PT - PR + 2G - 103 - 20 log(F) + 10 log(o)
40 log(D) = 87.8dBm - -92dBm + 2* 31.6dBi - 103 - 20 log (3000MHz) + 10 log(2sqrm)
40 log(D) = 87.8dBm + 92dBm +63.2dBi - 103 - 69.5dB + 3dBsm = 73.5dB
40 log(D) = 73.5dB
log(D) = 1.8375
D = 10^1.8375 = 69km <- ez bizony reális, örülünk.
T
Törölt tag 1945
Guest
No akkor fordítsuk komolyra a szót, és lássuk mennyire lehet egy adott analóg radar képességét számítással modellezni/előrejelezni.
Számoljunk egy SzA-75M Dvina tűzvezető lokátor átlagos MiG-21 felderítési távolságát.
Első lépés a hőzaj kiszámítása: kTB
Boltzmann állandó: k=1.38*10^-23 joule/K°
Üzemi hőmérséklet: T=290K° (17C°)
10 * log (kTB) = 10 * log (1.38 * 10^-23 joule/K° * 290K° * 1MHz) = 10 * log (4*10^-15) = -144dBW = -114dBm
Itt saccolunk egyet
tipikus zaj: 5dB
tipikus jel zaj viszony: 13dB
összesen tehát a hőzaj: -114dBm + 5dB + 13dB = -96dBm ami 1MHz sávszélességre érvényes, 17C° hőmérsékleten.
A Dvina komplexum V-750V légvédelmi rakétájának 196kg-os harci része 60m-en belül garantáltan hatásos, így ebből a komplexum számára szükséges távolság mérés pontosságára 120m adódik.
Tudjuk hogy 120m-t a fény 0.4μs alatt tesz meg, így a vevő szükséges sávszélessége kiszámolható:
B = 1/0.4μs = 2.5Mhz
Ebből már lehet becsülni egy átlagos vevőérzékenységet:
PR = -96dB + 10*log(2.5) = -92dBm
A Dvina tűzvezető lokátora 10° x 2° fokos legyezőnyalábot állít elő.
Számítsuk ki az antenna nyereséget.
o1, o2 - nyalábátmérő
G= 10*log(29000/((o1 * o2)) = 10*log(29000/((10° * 2°)) = 31.6dBi
A Dvina adó csúcsteljesítménye; 600kW = 600'000'000mW
PT = 10 * log (600'000'000mW) = 87.8dBm
És akkor jöhet az általános radaregyenlet:
PR = PT + 2G - 103 - 40 log(D) - 20 log(F) + 10 log(o)
ahol
PR - vételi teljesítmény (érzékenység); -92dBm
PT - adóteljesítmény; 87.8dBm
G - antenna nyereség; 31.6dBi
D - felderítési távolság; ezt keressük
F - frekvencia; 3GHz = 3000MHz
o - MiG-21 cél radarkeresztmetszete; 2m²
Az átlagos felderítési távolságra vagyok kíváncsi, az egyenletet átrendezem:
40 log(D) = PT - PR + 2G - 103 - 20 log(F) + 10 log(o)
40 log(D) = 87.8dBm - -92dBm + 2* 31.6dBi - 103 - 20 log (3000MHz) + 10 log(2sqrm)
40 log(D) = 87.8dBm + 92dBm +63.2dBi - 103 - 69.5dB + 3dBsm = 73.5dB
40 log(D) = 73.5dB
log(D) = 1.8375
D = 10^1.8375 = 69km <- ez bizony reális, örülünk.
A Dvina (SA-2A/B) tűzvezető lokátorának felderítő képességét a fenti egyenlettel könnyen kiszámíthatjuk mondjuk 1m²-es radar-keresztmetszetű célra is.
40 log(D) = PT - PR + 2G - 103 - 20 log(F) + 10 log(o)
40 log(D) = 87.8dBm - -92dBm + 2* 31.6dBi - 103 - 20 log (3000MHz) + 10 log(1m²)
40 log(D) = 87.8dBm + 92dBm +63.2dBi - 103 - 69.5dB + 0dBsm = 70.5dB
40 log(D) = 70.5dB
log(D) = 1.7616
D = 10^1.7616 = 58km
Nézzük most meg az egyenlet segítségével, hogy mit tehetünk a Dvina (SA-2A/B) lokátorunkkal, ha növelni szeretnénk a felderítési távolságát egyharmaddal, hogy a végén megkapjuk a Gyeszna (SA-2C) tűzvezető lokátorát.
PT - adóteljesítmény; 87.8dBm (600kW)
PR - vételi teljesítmény (érzékenység); -92dBm
2G - antenna nyereség duplája (adáskor és vételkor); 63,2dBi
F - frekvencia; 3GHz = 3000MHz
o - cél radarkeresztmetszete; 1m²
D - ~60km felderítési távolság; ezt szeretnénk egyharmaddal növelni, legyen a cél mondjuk ~80km
40 log(D) = 40 log(80km) = 76.5dB
Látható hogy +6dB-t kell a Dvinához (70.5dB) képest találnunk.
Első lépés az adóteljesítmény növelése.
Növeljük az adóteljesítményt kétharmaddal: 600kW->1000kW
PT = 10*log (1'000'000'000mW) = 90dBm
A Dvina 87.8dBm értékéhez képest 2.2dBm-et nyertünk a szükséges 6dB-ből.
T
Törölt tag 1945
Guest
Második lépésként vizsgáljuk meg a analóg vételi érzékenység növelésének lehetőségét.
Az analóg vételi érzékenységet azonos technikai színvonalon, leginkább a komplexum távolságmérési felbontásának növelésével lehetne növelni, ez azonban nagyobb harcirészt és ezáltal nagyobb tömregű rakétát igényelne.
Dvina (SA-2A/B) esetén a ~200kg-os harci rész ~60m-es mellélövés esetén garantál találatot, ami lehet ±60m, így összesen 120m-es szükséges távolságmérési felbontással számolva:
PR = -96dB + 10*log(300/120m) = -92dBm
Érdekességként nézzük meg a Berkut (SA-1) rakétájának ~400kg-os dupla tömegű harci részével mit nyerhetnénk. A dupla tömegű harci rész, mindössze negyed akkora távolsággal növeli a garantál megsemmisítési zónát 75m-re.
PR = -96dB + 10*log(300/150m) = -93dBm
A fentiekből látható, hogy nincs sok értelme a harcirész további növelésének, hiszen azt duplázva is mindössze 1dB-t nyernénk, nem beszélve annak hatásával a rakéta össztömegének növekedésére (azonos hatótávolságot feltételezve), ami új indítóállványt, töltő járművet, stb igényelne. Ez az út nem járható.
Az adón és a vevőn kívül maradt az antenna és annak nyeresége, ahol a szükséges 6dB-ből a hiányzó további 3.8dB-t kell a továbbiakban megtalálnunk.
T
Törölt tag 1945
Guest
Egy adott méretű antenna által kisugárzott nyaláb átmérője függ az antenna méretétől, illetve a nyaláb frekvenciájától. Ugyanakkora méretű antenna nagyobb frekvenciájú jelet, szűkebb nyalábba képes kisugározni. Kézenfekvőnek tűnhet az adó frekvenciájának növelése, viszont a magasabb frekvenciájú jelnek azonban nagyobb a terjedési vesztesége így valamennyit veszítünk az antenna nyereségének növelése esetén.
Növeljük az adó frekvenciát kétharmaddal, 3GHz-ről 5GHz-re.
Dvina (SA-2A/B) esetén a terjedési veszteség:
20 log(F) = 20 log (3000MHz) = 69.5dB
Gyeszna (SA-2C) esetén ugyanez:
20 log(F) = 20 log (5000MHz) = 74dB
Látható hogy a frekvencia kétharmaddal való növelése 4.5dB-el növeli a terjedési veszteségünket, lássuk mit nyerünk cserébe az antenna nyereségen.
A Dvina (SA-2A/B) antennája 10° x 2° fokos legyezőnyalábot állít elő, 3GHz-en.
Dvina nyeresége (duplán számolva, mivel az adás, és a vétel is ugyanazon az antennán valósul meg):
2G= 20*log(29000/(o1 * o2)) = 20*log(29000/(10° * 2°)) = 20*log(1450) = 63.2dBi
Az ugyanekkora méretű Gyeszna (SA-2C) antennája 5GHz-en már 7° x 1.1° fokos legyezőnyalábot állít elő.
2G= 20*log(29000/(o1 * o2)) = 20*log(29000/(7° x 1.1°)) = 20*log(3766) = 71.5dBi
Összesítve a frekvencia kétharmaddal történő növelése, 71.5dBi-63.2dBi = 8.3dB antenna nyereséget eredményezett, amit a terjedési veszteség a korábban célként kitűzött 8.3dBi-4.5dB = 3.8dB-re csökkent.
A fentieket összefoglalva, a felderítési távolság egyharmaddal való növeléséhez, az adóteljesítményt és a frekvenciát is kétharmaddal kellett növelni, az antenna méretének megtartásával.
A Gyeszna (SA-2C) adatai így:
PT - adóteljesítmény; 90dBm (1000kW)
PR - vételi teljesítmény (érzékenység); -92dBm
2G - antenna nyereség duplája (adáskor és vételkor); 71.5dBi (7° x 1.1°)
F - frekvencia függő terjedési veszteség; 74dB (3GHz)
o - cél radar-keresztmetszete; 0dB (1m²)
40 log(D) = PT - PR + 2G - 103 - 20 log(F) + 10 log(o)
40 log(D) = 90dBm - -92dBm + 71.5dBi - 103 - 74dB + 0 = 76.5dB
log(D) = 1.912
D = 10^1.7616 = 82km
Miután a fenti munkánkért kijáró Lenin rendet átvettük, a következő plecsniért tovább kell növelnünk a felderítési távolságot, azonban immár kétharmaddal...
T
Törölt tag 1945
Guest
Mivel a Volhov (SA-2D/E) fejlesztése során sem annak frekvenciáját, sem adóteljesítményét nem akarták tovább növelni, így a Gyesznához (SA-2C) képest kétharmaddal növelt felderítési távolságot csak új antenna hozzáadásával lehetett elérni. Ezek lettek az első tűnyalábot képző antennák a Szovjetunió tűzvezető lokátorai között.
Az elvárt 133km-es felderítési távolsághoz számítsuk ki, hogy mennyi extra dB-t kell az új antennán nyernünk...
40 log(D) = 40 log(133km) = 85dB
...mivel a Gyeszna esetén a fenti képlet eredménye 76.5dB volt, a szükséges különbség:
85dB - 76.5dB = 8.5dB
A Gyeszna antennája 7° x 1.1° nyalábot képezett...
2G= 20*log(29000/(o1 * o2)) = 20*log(29000/(7° x 1.1°)) = 20*log(3766) = 71.5dBi
... az új tűnyalábot létrehozó antennának így 71.5db + 8.5dB = 80dB-t kell teljesítenie.
Számítsuk ki a szükséges tűnyaláb átmérőjét.
80dB = 20*log(29000/o²)
4 = log(29000/o²)
10^4 = 29000/o²
o² = 29000/10000
o² = 2.9
o = 1.7°
Így kerültek fel a Volhov (SA-2D/E) keskenysugarú antennái.
T
Törölt tag 1945
Guest
Az SA-2-t itt befejeztem, de ha írok másik komplexumokról is, akkor azt ott folytatom, viszont nem akarom az alapoktól kezdeni.
T
Törölt tag 1945
Guest
T
Törölt tag 1945
Guest
Érdekes elgondolás hk alvázra tenni kubai viszonyok közt. Én inkább nyergessel próbálkoztam volna.
A kezdetek - 1D rakéta szerelőkocsin
TZM-n
Indító állványon
Levegőben
Tipikus osztály telepítés
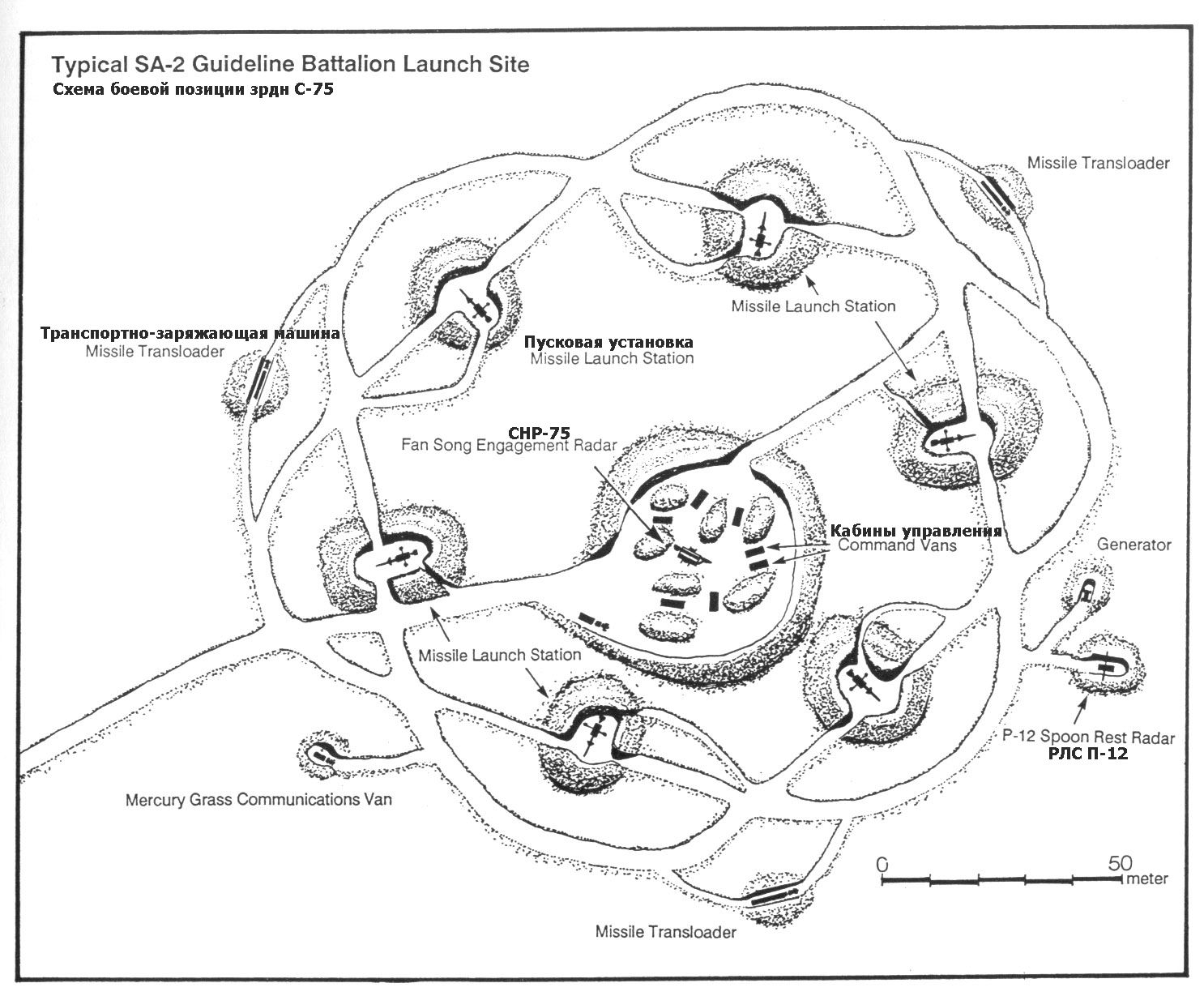
TZM-n
Indító állványon
Levegőben
Tipikus osztály telepítés
Román 5Ja23 rakéta Zil-131 TZM-n
SzM-90 indító állványon
Töltés
Harci munka az UV kabinban
SzM-90 indító állványon
Töltés
Harci munka az UV kabinban
ZiL-131 TZM 5Ja-23 rakétával
9S33A Televíziós-optika
Sz-75M4 (1978) - RSZN-75V4
9S33A Televíziós-optika
Sz-75M4 (1978) - RSZN-75V4