A gondolatba belelátás és az álmok leképezése már folyamatban van.Kezdjük a közismert és a hidegháború alatt rendszeresített eszközöktől, és haladjunk azon a technikák felé, melyek kevésbé ismertek, esetleg vélhetően rendszeresített eszközeik jelenleg is minősítettek, vagy csak elméleti lehetőségként léteznek.
Következzenek a rendszeresített mágneses anomália detektorok.
- AN/ASQ-10
- AN/ASQ-81
- AN/ASQ-208
- AN/ASQ-233
A mágneses mező mértékegysége a Tesla.

Egy Tesla azonban túl sok, így amikor a föld mágneses teréről beszélünk ennek milliárdod részét, a nano Tesla-t (nT) használják a civil tudományban.
Hogy leegyszerűsítsék a dolgukat, a milliárdod helyett a katonai irodalom egy nano Tesla-t (nT) egy gammának (γ) nevez.
Egy kis hatványozás...
1mT (egy mili-Tesla) = 0.001T – egy ezred Tesla
1μT (egy mikro-Tesla) = 0.000’001T – egy milliomod Tesla= 1’000γ (ezer gamma)
1nT (egy nano-Tesla) = 0.000’000’001T – egy milliárdod (ezer-milliomod) Tesla = 1γ (gamma)
1pT (egy piko-Tesla) = 0.000’000’000’001T – egy billiómod (milliomod-millioma) Tesla = 0.001 γ (egy ezred gamma)
1fT (egy femto-Tesla) = 0.000’000’000’000’001T – egy ezredbilliómod Tesla
Mivel mind civil, mind katonai szakirodalmat használok, így forrás függően, vegyesen alkalmazom majd mindkét mértékegységet, de a lényeg, hogy 1nT (nano Tesla) = 1γ (gamma).
A föld mágneses tere erősen változik a geográfiai pozíciótól függően.

Maximuma a Déli sarkon 68’000γ, az északi féltekén a Sziklás hegység környékén és az Urálon túli területeken 60’000γ.
Minimuma a “Dél Atlanti Anomália” fölött mindössze 25’000γ.
A hadászatilag érdekes;
- Atlanti óceán északi részén, az Északi, és a Barents tengeren a mező ereje 45’000…55’000γ közötti.
- Csendes óceán északi részén, az Ohotszki, és a Bering tengeren a mező ereje 35’000…57’500γ közötti.
Minden a föld mágneses terébe helyezett mágnesezhető tárgy visszahat a föld mágneses terére, és abban anomáliát okoz.
Ennek a hatásnak (anomáliának) a nagysága a tárgy hosszától függ.

(A) föld mágneses tere.
(B) föld mágneses tere a mágnesezhető tárgyon két pólust indukál.
Ha sokáig ugyanebben a pozícióban állna a cél (például egy kikötőben), akkor felmágneseződne, de itt ez még nem történt meg.
(C) A célon lévő két pólus, hatással van a föld mágneses terére, anomáliát okoz - torzítja azt.
(D) Az anomálián átrepülő felderítő a mágneses tér szinuszos változását észleli a cél fölött.
Lássuk, hogy egyes tárgyak mennyire befolyásolják a föld 68’000nT és 25’000nT közötti mágneses terét:
- távvezeték; 100nT
- egy autó 50m távolságban; 5nT
- tengeralattjáró 150m távolságban; 4γ
- tengeralattjáró 200m távolságban; 1.6γ
- csavarhúzó 5m távolságban; 0.5nT
- mikroprocesszor 2m távolságban; 1pT (piko Tesla – ezred nano-Tesla)
- emberi agyhullámok pár cm távolságban; 50fT (femto Tesla – milliomod nano-Tesla)
A föld mágneses mezejének erőssége korántsem állandó, és katonai szempontból persze nem a párszázezer évente történő pólusváltás érdekes, hanem az annál gyorsabban lejátszódó jelenségek.

A napkitörések által okozott mágneses viharok, percek alatt, véletlenszerűen 100nT mértékben változtatják a föld mágneses terét.
Mágneses viharok idején, napokon át használhatatlanok a mágneses anomália detektorok.

Napkitörések száma a 12 éves napciklustól függ.
Csúcsévben akár másfél hónapon át, csendes évben összesen két hétig kell lemondani a mágneses anomália detektor használatáról.

A föld mágneses tere napi szinten is változik, az ionoszféra pillanatnyi állapotának függvényében.

Part menti vizeken a civil tevékenység jelentős 5..50γ közötti zajt okoz, így itt a mágneses anomália detektor csak korlátozottan használható, mivel a mágneses zaj elnyomja a tengeralattjáró által okozott anomáliát, ami 150m távolságban 4γ, 200m távolságban már csak 1.6γ.
A továbbiakban a hidegháború alatt alkalmazott konkrét mágneses anomália detektor típusokról, és működési elveikről lessz szó, némi kitekintéssel a jövő rendszereinek a jelenleg csak elméleti lehetőségeire.
Csak úgy potyognak majd a Nobel díjak, és kiderül, hogy a jövőbeli fedélzeti (szupravezetőn alapuló kvantum interferencia) MAD operátor tényleg belelát-e a pilótalány gondolataiba.

You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
1x10⁻⁴ W/m²
Hajópropellerek által okozott biolumineszcencia a tengerben
Egyetlen páncélos ostoros plankton állatka, ha megzavarják (és emiatt jól megmérgelődik), átlagosan 2pW (piko Watt – 2x10¯¹²W) fényenergiát bocsájt ki.
Élőhelytől (és évszaktól) függ, hogy mennyi található belőlük egy liter vízben:
- Ohotszki tengeren; ~100’000db/l
- Atlanti óceánon; ~10’000db/l
- Csendes óceánon; ~1’000db/l

Becsüljük meg egy 5m átmérőjű, lassan forgó hajócsavarral rendelkező atomtengeralattjáró által megzavart Dinoflagelláták által kibocsájtott fény energiáját az Ohotszki tengeren:
Tengeralattjáró hajócsavar becsült átmérője: 5m
Egyetlen Dinoflagelláta által kibocsájtott maximális fényerő: 2x10¯¹²W
Egyetlen Dinoflagelláta által kibocsájtott maximális fényerő időtartalma: 0.1s
Dinoflagelláták átlagos száma az Ohotszki tengeren: 100’000db/l
Egy köbméter az ezer liter: 1000l/m³
5m x 2x10¯¹²W x 0.1s x 100’000db/l x 1000l/m³ = 1x10⁻⁴ W/m²
A fenti becslés, az Ohotszki tengerre vonatkozik, az Atlanti óceánon 1x10⁻⁵ W/m², a Csendes óceánon pedig 1x10⁻⁶ W/m².
(természetesen időszakosan kialakulhat sűrűbb Dinoflagelláta populáció is helytől, táplálék mennyiségtől és évszaktól függően)
Ahhoz hogy műholdról, vagy repülőről felderíthessük a tengeralattjárók hajócsavarja által okozott kékes derengést, annak erősebbnek kell lennie, mint a tenger felszínéről visszaverődő napfény/holdfény/stb (zaj).
Újholdkor, teljesen felhőmentes sötét éjszaka, a felszínt 10mW/m² fény éri.
A tenger hullámzásán azonban szóródik a fény, így számoljunk csak a képzeletbeli műholdunk felé, a tenger felszín visszaverődésének 1%-val: 1x10¯⁴ W/m²
A fenti számításból látható, hogy az Ohotszki tengeren a Dinoflagelláták átlagos fénye csak újholdkor észlelhető a felszín közelében.
A biolumineszcencia jelensége így véleményem szerint csak tökéletesen tiszta sötét éjszakán használható műholdról tengeralattjáró felderítésre, ha az közvetlen a felszín alatt halad - periszkópmélységben, és sodorhulláma a felszínt érinti.

A Dinoflagelláta alapú eredményes tengeralattjáró felderítés legfőbb akadályának a planktonok által kibocsájtott fény alacsony teljesítménye tűnik...
... azonban ha nagy teljesítményű lézerrel világítanánk a tenger alá, akkor már mindjárt más lenne a helyzet.
1x10⁻⁴ W/m²
Ez Ws/m²-ben fog kijönni, nem? Ráadásul a tengeralattjáró közben halad is így a hajócsavar több vizet kavar fel.
Következzék a kék lézer alapú LIDAR, amivel tán kevéssé ismert, de már tényleg detektáltak idegen tengeralattjárót...
Ez Ws/m²-ben fog kijönni, nem? Ráadásul a tengeralattjáró közben halad is így a hajócsavar több vizet kavar fel.
Szinszűrővel szerintem éjszaka akár műholdról is megy ez.
Amikor a bevetési helyükre mennek. Ha megérkeznek, igyekeznek eltünni.De hol szálguldoznak ennyivel?Az óceán közepén vagy ott ahol van is valami?
És amikor flottákat vagy hajókat követnek.
T
Törölt tag
Guest
Urak,
Az elmúlt két évben írogattam a fórumba pár sorozatot, a tengeralattjáró illetve hajófedélzeti szonárok, szonárbóják, torpedók, reaktorok, illetve ezek háborús körülmények közötti alkalmazásáról 1982-ben a Falkland szigeteki konfliktusban.
Mindez magyarul eddig még tán nem jelent meg, így összedobáltam ezeket a hozzászólásokat egy PDF-be, 250Mb, és valami 550 oldal lett.
http://www.mediafire.com/file/r4ibkwffm1y97vb/SUBs.pdf
Jó olvasgatást!
Hpasp
Az elmúlt két évben írogattam a fórumba pár sorozatot, a tengeralattjáró illetve hajófedélzeti szonárok, szonárbóják, torpedók, reaktorok, illetve ezek háborús körülmények közötti alkalmazásáról 1982-ben a Falkland szigeteki konfliktusban.
Mindez magyarul eddig még tán nem jelent meg, így összedobáltam ezeket a hozzászólásokat egy PDF-be, 250Mb, és valami 550 oldal lett.
http://www.mediafire.com/file/r4ibkwffm1y97vb/SUBs.pdf
Jó olvasgatást!
Hpasp
T
Törölt tag
Guest
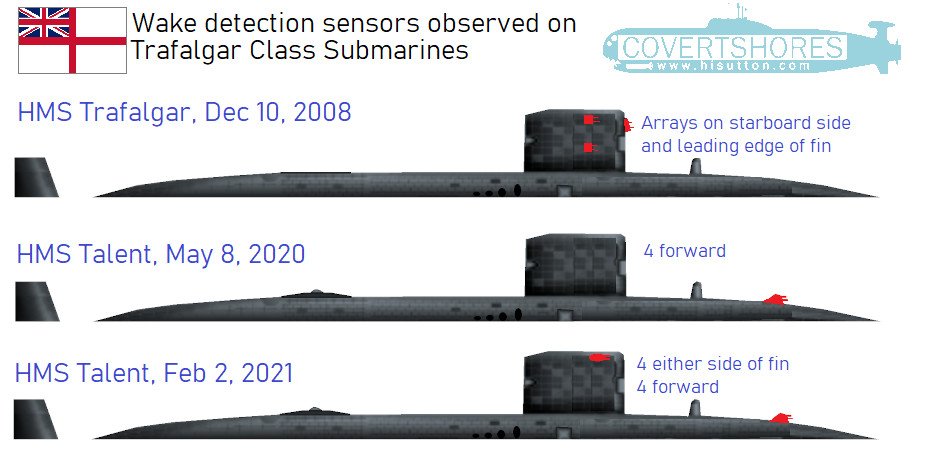
Ha már a Britek megszerezték úgy tűnik tovább is fejlesztették a SOKS rendszert.Úgy tűnik a Brit vadász tengókon is megelentek az Orosz SOKS hoz hasonló hasonló wake detection rendszerek


https://www.thedrive.com/the-war-zo...oyal-navy-submarine-as-it-pulls-ito-gibraltar

Mikor szerezték meg?Ha már a Britek megszerezték úgy tűnik tovább is fejlesztették a SOKS rendszert.
https://www.thedrive.com/the-war-zo...oyal-navy-submarine-as-it-pulls-ito-gibraltar

T
Törölt tag
Guest
Először tavaly májusban bukkant fel egy Brit tengón az Orosz SOKS rendszerhez kísértetiesen hasonló hullám detektor rendszer érzékelőiMikor szerezték meg?
Az eredeti orosz:

Úgy értem: van valami ami arra utal, hogy "szerezték", és nem maguktól fejlesztették ki?Először tavaly májusban bukkant fel egy Brit tengón az Orosz SOKS rendszerhez kísértetiesen hasonló hullám detektor rendszer érzékelői
Az eredeti orosz:

T
Törölt tag
Guest
Műhódról alkalmazható lézernek nagyon kis fogyasztásúnak, és nagyon nagy impulzus-sűrűségűnek kell lennie. Hát egy műhold nagyon gyorsan halad, és a tengeralattjáró meg nagyon pici. Ahoz, hogy értékelhető felbontásban keresgéljen mondjuk egy 50 km-es sávban, másodpercenként kb 500E impulzus kellene. Ha egy impulzus mondjuk 1W, akkor ez 500 kW másodpercenként.LIDAR (Light Detection and Ranging)

Nemrég egy új kínai tengeralattjáró felderítő műhold elképzelés “Project Guanlan” esetében került közérdeklődés terébe a LIDAR alkalmazásával történő tengeralattjáró felderítés.
Pár sajtó által említett konkrétum...
Az Egyesült Államok és a volt Szovjetunió által a hidegháborúban végzett kísérletekben (nyíltan elérhető információk szerint) 100 méternél kevesebb detektálási mélységet értek el az űrből.
A DARPA által kifejlesztett eszközt repülőre szerelve 200 méteres mélységben megbízható eredményeket értek el olyan kis célokkal szemben is, mint a tengeri aknák.
https://www.businessinsider.com/chi...satellite-could-track-subs-underwater-2018-10
A Pentagon DARPA védelmi fejlesztési projektje (DARPA) által létrehozott lézerberendezés megbízható eredményeket szolgáltat 200 méter mélységben.
https://sputniknews.com/military/201810021068501835-china-submarine-laser-satellite/
A Guanlan projekt ("a nagy hullámok figyelése") célja egy olyan műhold létrehozása, amely észleli a tengeralattjárókat 500 méteres mélységben, ami sokkal több, mint amit az Egyesült Államok és Oroszország korábban elért.
https://nationalinterest.org/blog/b...satellite-spot-and-help-kill-submarines-33406
LIDAR alapú tengeralattjáró észlelés témájában tán kevéssé ismert...
... hogy az amerikai haditengerészet 1969-óta használja a part menti vizek feltérképezésére repülő fedélzeti LIDAR-t.

Mostanában éppen a Szaúdi Arábiai Jeddah kikötője körül dolgoztak.

1981 októberében a Svédország közvéleménye arra ébredt, hogy egy pr613-as (Whiskey) osztályú szovjet vadász tengeralattjáró (S-363) megfeneklett a part menti felségvizeiken, alig 10km-re a Svéd haditengerészet Karlskronai bázisától.
https://www.warhistoryonline.com/wa...find-a-russian-submarine-stuck-on-a-rock.html

A szovjetek persze szokás szerint hivatkoztak navigációs hibára, különböző fedélzeti berendezések meghibásodása által okozott vészhelyzetekre, és a többi, a diplomaták számára előre bekészített marhaságra.

Az incidens után a svéd haditengerészet az "Operation Notvarp" keretében műszaki zárat telepített kikötői elé, és már 1982 őszén a “Hårsfjärden Incidens” alatt, feltételezhetően LIDAR érzékelők segítségével észlelt a sekély vízben egy a Hårsfjärden kikötője előtt navigáló, azonosítatlan idegen tengeralattjárót, amire több éles vízibombát dobtak. (eredmény nélkül)

A nyolcvanas években a svéd felségvizeket szinte folyamatosan megsértették idegen tengeralattjárók.
(amik észlelésében segíthettek a Svéd LIDAR műszaki zárak)
https://sv.wikipedia.org/wiki/Ubåtskränkningar_i_Sverige
A LIDAR alapú tengeralattjáró észlelés témája igazán aktuális ahhoz, hogy fizikai és matematikai szempontból is megismerjük/megértsük.
A harmadik világháború a tervek szerint két napig tartana.Szerintem inkább a rugalmasság a hadászati bombázók fő életben tartója.SSBN járórözhet a réteghatár és/vagy a jég alatt,felderithetetlenül.A mobil szárazföldi hadászati rakéták meg szintén szétspriccelhetnek,még atombiztos bunkerekbe is rejthetők.Viszont csak a végső és utolsó érvet jelentik.Gyakorlatilag bevethetetlenek.A bombázók jobban alkalmazhatók a mindennapok politikai és hadszintéri harcaiban.A hipotetikus III.vh-ban,abban a max 1órában amig tartana,el se jutnának a fegyverzetük bevetéséig.Amelyik mégis,az meg már minek,mit támadjon?Fekete üveget?
A hibaszázalékot meg jól jelzi az egy hónapon keresztül hajkurászott nem létező tengeralattjáró.LIDAR (Light Detection and Ranging)

Nemrég egy új kínai tengeralattjáró felderítő műhold elképzelés “Project Guanlan” esetében került közérdeklődés terébe a LIDAR alkalmazásával történő tengeralattjáró felderítés.
Pár sajtó által említett konkrétum...
Az Egyesült Államok és a volt Szovjetunió által a hidegháborúban végzett kísérletekben (nyíltan elérhető információk szerint) 100 méternél kevesebb detektálási mélységet értek el az űrből.
A DARPA által kifejlesztett eszközt repülőre szerelve 200 méteres mélységben megbízható eredményeket értek el olyan kis célokkal szemben is, mint a tengeri aknák.
https://www.businessinsider.com/chi...satellite-could-track-subs-underwater-2018-10
A Pentagon DARPA védelmi fejlesztési projektje (DARPA) által létrehozott lézerberendezés megbízható eredményeket szolgáltat 200 méter mélységben.
https://sputniknews.com/military/201810021068501835-china-submarine-laser-satellite/
A Guanlan projekt ("a nagy hullámok figyelése") célja egy olyan műhold létrehozása, amely észleli a tengeralattjárókat 500 méteres mélységben, ami sokkal több, mint amit az Egyesült Államok és Oroszország korábban elért.
https://nationalinterest.org/blog/b...satellite-spot-and-help-kill-submarines-33406
LIDAR alapú tengeralattjáró észlelés témájában tán kevéssé ismert...
... hogy az amerikai haditengerészet 1969-óta használja a part menti vizek feltérképezésére repülő fedélzeti LIDAR-t.

Mostanában éppen a Szaúdi Arábiai Jeddah kikötője körül dolgoztak.

1981 októberében a Svédország közvéleménye arra ébredt, hogy egy pr613-as (Whiskey) osztályú szovjet vadász tengeralattjáró (S-363) megfeneklett a part menti felségvizeiken, alig 10km-re a Svéd haditengerészet Karlskronai bázisától.
https://www.warhistoryonline.com/wa...find-a-russian-submarine-stuck-on-a-rock.html

A szovjetek persze szokás szerint hivatkoztak navigációs hibára, különböző fedélzeti berendezések meghibásodása által okozott vészhelyzetekre, és a többi, a diplomaták számára előre bekészített marhaságra.

Az incidens után a svéd haditengerészet az "Operation Notvarp" keretében műszaki zárat telepített kikötői elé, és már 1982 őszén a “Hårsfjärden Incidens” alatt, feltételezhetően LIDAR érzékelők segítségével észlelt a sekély vízben egy a Hårsfjärden kikötője előtt navigáló, azonosítatlan idegen tengeralattjárót, amire több éles vízibombát dobtak. (eredmény nélkül)

A nyolcvanas években a svéd felségvizeket szinte folyamatosan megsértették idegen tengeralattjárók.
(amik észlelésében segíthettek a Svéd LIDAR műszaki zárak)
https://sv.wikipedia.org/wiki/Ubåtskränkningar_i_Sverige
A LIDAR alapú tengeralattjáró észlelés témája igazán aktuális ahhoz, hogy fizikai és matematikai szempontból is megismerjük/megértsük.
"és a műhold 500Hz ismétlődési frekvenciával dolgozik."Előre is elnézést kérek, de itt némileg hosszabb matek következik...

Egy űrbe telepített lézernek elég erősnek kell lennie, hogy a kétszeres (oda-vissza) légköri és vízalatti elnyelődés után is a célról visszavert jel erősebb legyen mint a tenger felszínén megcsillanó természetes háttér világítás (nap, hold, stb).
A lézer hullámhosszát úgy kell kiválasztani, hogy annak fénye a legkevésbé szóródjon a tengerben.
A korábban emlegetett Dinoflagelláták jobban értenek a fizikához nálam, ami abból is kiderül, hogy pont az általuk használt fény (0.42...0.59μm) nyelődik el a legkevésbé az óceánban.
Higany-Bromid lézer jó választás lehet erre a célra, mivel hullámhossza pont (0.49...0.51μm).
Esetleg egyéb egzotikus lézerek is szóba jöhetnek, úgy mint Xenon-Klorid, optikailag pumpált Neodímium, esetleg Réz-gőz.
0..75m mélység között a fény 11.17%-a nyelődik el méterenként, a 0.42...0.59μm tartományban. 75..150m között 7.21%, 150m alatt már csak 4.83%.
Számítsuk ki a vízalatti oda-vissza veszteséget adott mélységre:
Mélység: 50m
Elnyelődés: 11.17%/m
Fénymennyiség, ami nem nyelődik el: 1-11.17%/m = 88.83%/m
Maradék fénymennyiség 50m-en: 88.83%/m^(50m) = 0.2679%
Veszteség 50m-en decibelben kifejezve: 10*log (0.2679%) = -25.7dB
Veszteség oda-vissza decibelben kifejezve (50m-re): -25.7dB x 2 = -51dB
A fenti veszteségszámításokat elvégezve több mélységre:
50m; -51dB
75m; -72dB
100m; -91dB
150m; -124dB
200m; -145dB
250m; -167dB
300m; -189dB
Űrben telepített eszköz számára a folyamatosan változó légkör is veszteségeket okoz.
Az óceánok 75%-át felhők takarják, 10 napból átlagosan 6-on, (az Atlanti óceán északi részén 10 napból átlagosan 8 napon át).
A számunkra érdekes 0.42...0.59μm tartományban a légköri oda-vissza út elnyelődés mértéke:
Tiszta időben; -4dB
Párás időben; -10dB
Ködös időben; -14dB
Felhős időben; -26dB
Felhős+ködös időben; -40dB
A műhold LIDAR-ja által kibocsájtott fényimpulzusnak a fenti elnyelődések után is erősebbnek kell maradnia, mint a tenger felszínén megcsillanó természetes háttér világításnak (nap, hold, stb), ami:
Napsütés esetén: 1000 W/m²
Teljes borultság esetén: 100 W/m²
Éjszaka telihold esetén: 10 mW/m²
Éjszaka teljes borultság esetén: 1 mW/m²
Mivel a tenger hullámzik, ami szórja a természetes háttér világítás fényét, így az eredeti értékek 1%-val számolunk.
(Ennyi verődik vissza pont a műholdunk felé.)
Napsütés esetén: 10 W/m²
Teljes borultság esetén: 1 W/m²
Éjszaka telihold esetén: 1 x10¯⁴ W/m²
Éjszaka teljes borultság esetén: 1 x10¯⁵ W/m²
Napos tiszta idő esetén a teljes számítás:
Tengerfelszínről a műholdba jutó energia (0.42...0.59μm tartományban, 1% felszíni hullám szóródással): 10W/ m²
Légköri (oda-vissza) elnyelődés (0.42...0.59μm tartományban): -4dB
Tengeri (oda-vissza) elnyelődés 50m mélységben (0.42...0.59μm tartományban): -51dB
Teljes (légkör+tenger 50m) oda-vissza elnyelődés: -4dB + -51dB = -55dB
Tengerfelszínről a műholdba jutó napfény a légköri elnyelődés (csak vissza) után: 10W x 10^(-2dB / 10) = 6W/m²
Azt szeretnénk kiszámolni, hogy mekkora kibocsájtott fényenergiára van szükség a műholdon ahhoz, hogy legalább 6W/m² fényenergia érkezzen vissza az 50m mélyen úszó célról: 6W / 10^(-55dB / 10) = 2MW/m²
A fenti 2MW/m² leadott fényimpulzus persze csak akkor lenne igaz, ha a cél felülete tökéletes tükröződne.
Számoljunk a reálisabb 1%-os visszaverődéssel a cél fekete festéséről: 2MW/m² / 1% = 200MW/m²
LIDAR lézerünk számára azonban felesleges 1m² nyalábbal dolgozni, elég lesz 1cm², amivel a szükséges fényimpulzus: 200MW/m² / 10’000 = 20kW/cm²
A fényimpulzus csúcsteljesítménye helyett azonban minket a szükséges elektromos átlagteljesítmény érdekel.
A céljel 15m távolsági felbontása esetén a szükséges fényimpulzus hossza:
2 x d / c = 2 x 15m / 300’000’000m/s = 100ns
Feltételezzük, hogy 1W Higany-Bromid lézer fényimpulzus előállításához 100W elektromos teljesítmény szükséges (100x), és a műhold 500Hz ismétlődési frekvenciával dolgozik.
A szükséges átlagos elektromos teljesítmény értéke így: 20kW/cm² x 100 x 500Hz x 100ns = 100W
a fenti szükséges elektromos átlagteljesítmény számításokat elvégezve több mélységre:

A Nemzetközi Űrállomást alapul véve, aminek napelemei átlagosan 100kW teljesítmény leadására képesek, megállapíthatjuk, hogy számításaink szerint nappal a reális felderítési mélység valahol 75m, éjszaka 100..150m körül lehet az időjárás függvényében.
Két személyes megjegyzés:
1, A fenti számítás célja a matematikai apparátus megismertetése volt, nem egy jövőbeni Kínai terv véleményezése a látatlanba.
2, Az hogy az újságok nem számolnak be róla, még nem jelenti, hogy jelenleg nem keringenek fent hasonló célú amerikai műholdak.

Csóri műhód másodpercenként 8 kmt tesz meg. De mondjuk csak 4et. ha 10 méterenként lő egyet az ugye 400 Hz. Hanem szegénynek szélességben is pásztázni kell, különben nem talál semmit. Ha mondjuk a szélesség 10 km, akkor másodpercenként már 400 ezret kell lőnie, nem?

Hajópropellerek által okozott biolumineszcencia a tengerben
Egyetlen páncélos ostoros plankton állatka, ha megzavarják (és emiatt jól megmérgelődik), átlagosan 2pW (piko Watt – 2x10¯¹²W) fényenergiát bocsájt ki.
Élőhelytől (és évszaktól) függ, hogy mennyi található belőlük egy liter vízben:
- Ohotszki tengeren; ~100’000db/l
- Atlanti óceánon; ~10’000db/l
- Csendes óceánon; ~1’000db/l

Becsüljük meg egy 5m átmérőjű, lassan forgó hajócsavarral rendelkező atomtengeralattjáró által megzavart Dinoflagelláták által kibocsájtott fény energiáját az Ohotszki tengeren:
Tengeralattjáró hajócsavar becsült átmérője: 5m
Egyetlen Dinoflagelláta által kibocsájtott maximális fényerő: 2x10¯¹²W
Egyetlen Dinoflagelláta által kibocsájtott maximális fényerő időtartalma: 0.1s
Dinoflagelláták átlagos száma az Ohotszki tengeren: 100’000db/l
Egy köbméter az ezer liter: 1000l/m³
5m x 2x10¯¹²W x 0.1s x 100’000db/l x 1000l/m³ = 1x10⁻⁴ W/m²
A fenti becslés, az Ohotszki tengerre vonatkozik, az Atlanti óceánon 1x10⁻⁵ W/m², a Csendes óceánon pedig 1x10⁻⁶ W/m².
(természetesen időszakosan kialakulhat sűrűbb Dinoflagelláta populáció is helytől, táplálék mennyiségtől és évszaktól függően)
Ahhoz hogy műholdról, vagy repülőről felderíthessük a tengeralattjárók hajócsavarja által okozott kékes derengést, annak erősebbnek kell lennie, mint a tenger felszínéről visszaverődő napfény/holdfény/stb (zaj).
Újholdkor, teljesen felhőmentes sötét éjszaka, a felszínt 10mW/m² fény éri.
A tenger hullámzásán azonban szóródik a fény, így számoljunk csak a képzeletbeli műholdunk felé, a tenger felszín visszaverődésének 1%-val: 1x10¯⁴ W/m²
A fenti számításból látható, hogy az Ohotszki tengeren a Dinoflagelláták átlagos fénye csak újholdkor észlelhető a felszín közelében.
A biolumineszcencia jelensége így véleményem szerint csak tökéletesen tiszta sötét éjszakán használható műholdról tengeralattjáró felderítésre, ha az közvetlen a felszín alatt halad - periszkópmélységben, és sodorhulláma a felszínt érinti.

A Dinoflagelláta alapú eredményes tengeralattjáró felderítés legfőbb akadályának a planktonok által kibocsájtott fény alacsony teljesítménye tűnik...
... azonban ha nagy teljesítményű lézerrel világítanánk a tenger alá, akkor már mindjárt más lenne a helyzet.
Az óceanográfusok több mint négy évtizede tanulmányozzák a biolumineszcens planktonokat. Becslések szerint a globális óceán biomasszájának háromnegyede biolumineszcens tulajdonságokkal rendelkezik. A plankton világít, amikor a víz körülötte felkavarodik, ami lehetővé teszi a tengeralattjárók észlelését különböző mélységekben az óceán nagy részén...
Napjainkban az újdonság abban állna, hogy a megfigyelőnek rajként működő, kis méretű, pilóta nélküli légi járművekre telepített maradékfény alatt működő fejlett optikai eszközöket alkalmaznának és a kapott képeket fejlett elemző algoritmusokkal vizsgálnák..
A Journal of Harbin Engineering University szakfolyóiratban közzétett eredmények szerint a Kelvin-féle ébredési hullámok által keltett mágneses nyomok még jóval azután is kimutathatók, hogy a tengeralattjáró elhagyta a területet. Ez az információ lehetővé teheti Kína számára, hogy valós időben kövesse a lopakodó tengeralattjárókat – természetesen a sekély vizekben is...


A legújabb kínai technológia képes érzékelni az amerikai lopakodó tengeralattjárókat is
A mágneses nyomon követés elől nincs menekvés, ráadásul Kína egyre inkább integrálja más technológiákkal is.
raketa.hu