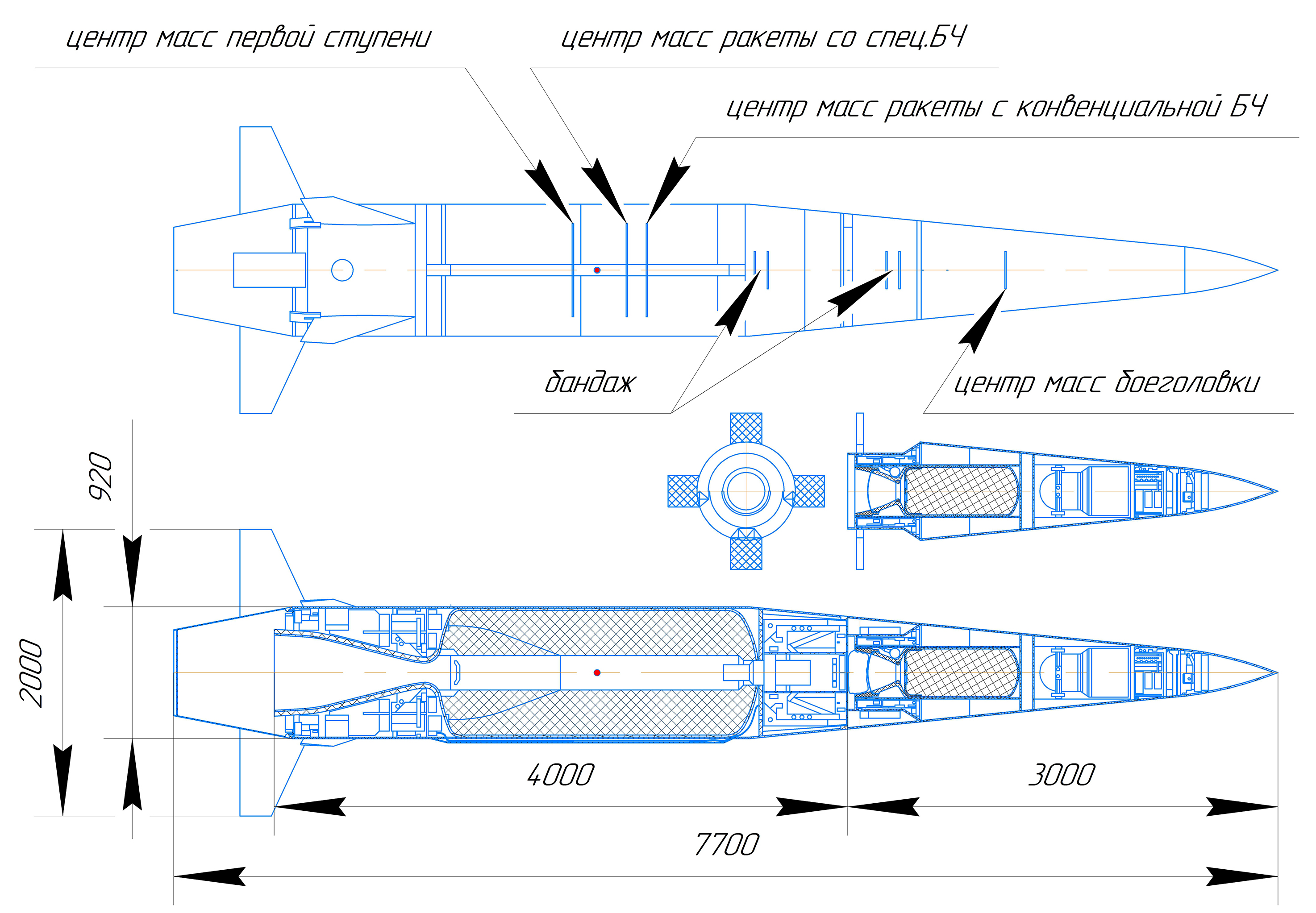
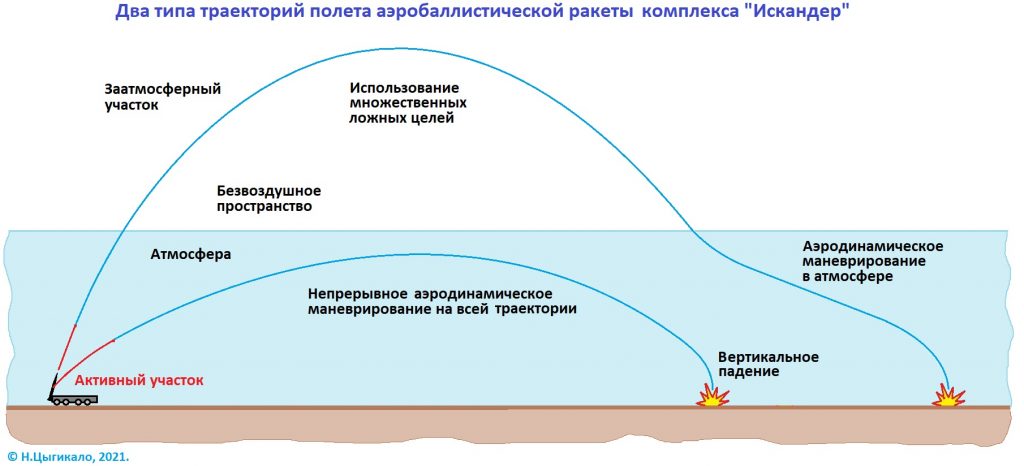
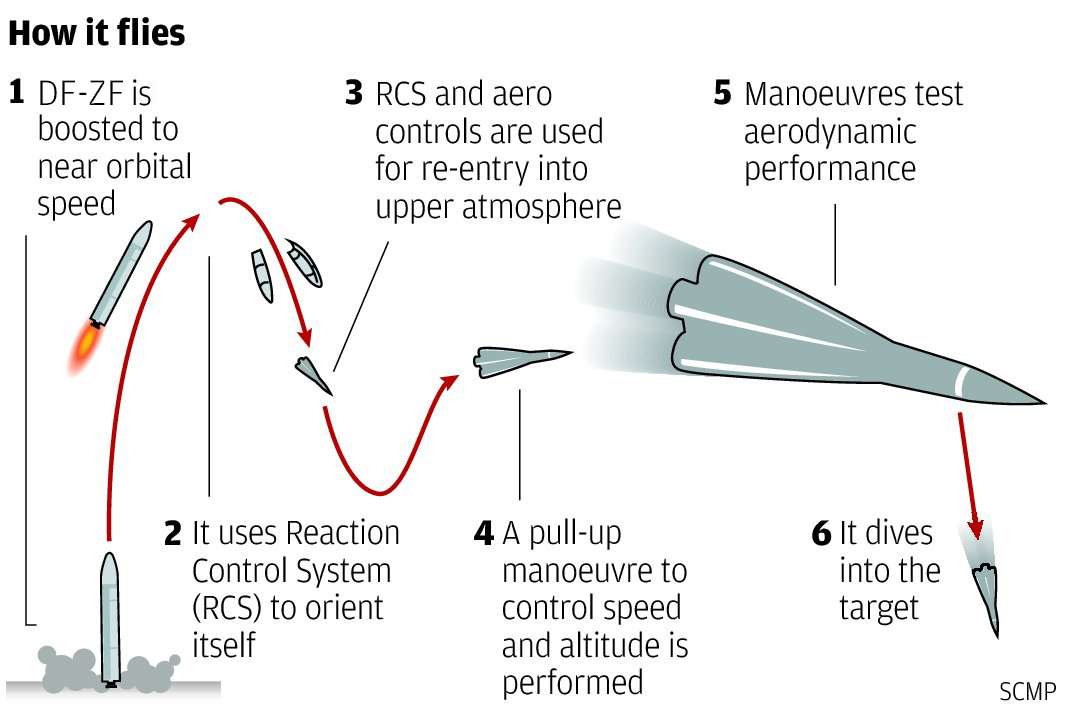
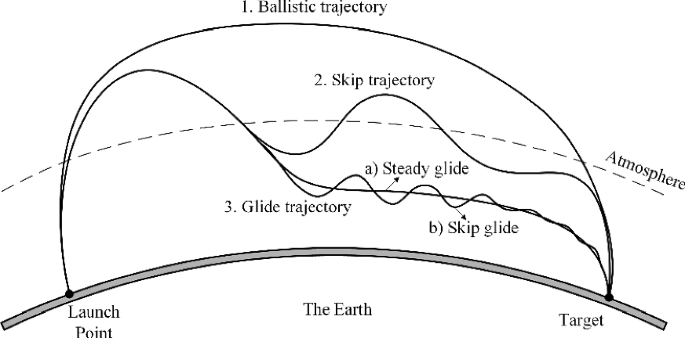
Amit írtam, azt az Avangard formájú hiperszonikus cuccokra írtam, viszont amit most írok, az érvényes minden térbeli testre.
Az erőhatásoknál ne felejtsük el, hogy ez egy térbeli cuccos. Vegyük példának a hullámvasútat. Jössz le a lejtőn, majd kimész egyenesen, közel 90fokos forduló, az átlagsebességed egy keveset változik, de itt sebesség- és gyorsuláskomponensek vannak. Ennél a fordulónál kb. 5G-t kapsz a hullámvasúton, viszont az 5G egy lefelé mutató komponens, van meg egy x és y irányú komponens. Az 5G az jelenti, hogy másodpercenként kb. 50m/s² lassulás van a z-koordinátában, az y-koordinátában szinte semmi változás, az x-koordináta meg 0-ról felmegy 1,2G-re, de az átlagsebességed változott kb. 3m/s-ot... (Ez hiperszonikus repülés esetében valószínűleg nagyobb érték...)
A helyes és precíz az lenne, ha minden egyes pillanathoz a sebesség és gyorsulás vektor lenne hozzárendelve és a helyzeti energia változás szintén meg lenne adva. A helyzeti energia megváltozása - légellenállás + booster (ha van) áll rendelkezésre. A sebességek megváltozása mindig a koordináták viszonylatában értendő. Itt biztosan lesz olyan sebességkomponens, amelyik csökken, lesz olyan, amelyik nő és lesz olyan, amelyik változatlan marad.
Betettem egy gyerek-hullámvasút foronómiai görbéit:
Ha megnézed, akkor a felső képen a piros vonal az x-irányú gyorsulás (x jelenti az előre irányt, y az oldalirány míg a z a lefelé mutató irány), vagyis a test 14 másodperctől 16,5 másodpercig a haladási irányban negatív gyorsulással (vagyis x-irányban fékez) halad, mégis gyorsul a helyzeti energia megváltozása miatt gyorsul.
Aztán 8 másodpercig folyamatosan gyorsul x-irányban, de a sebessége nem változik a hullámvasútnak, mert a helyzeti energia változását fedeznie kell - emiatt kell amúgy egy emelkedőn folyamatosan gyorsulni, ha ugyanazzal a sebességgel akarsz felmenni. Ez működik visszafelé is.
Amit ebből ki akartam hozni az az, hogy térbeli mozgásnál mindig hely-, sebesség- és gyorsulásvektorokról kell beszélni. Ha azt mondja valaki, hogy egy 10G-s manővert hajt végre, azt nem értem. 10G a gyorsulásvektor eredője, vagy 10G valamelyik irányvektor esetén.. Ha "simán" 10G a gyorsulása egy testnek, akkor lehet, hogy pl. 5,7G gyorsulása van
mind a három koordináta irányában, egyszerre. Így azt mondani, hogy egy rakétára hat 5G akkor az 5G=centripetális gyorsulás, teljesen hibás. 5G melyik irányokban hat? És a komponensek fogják definiálni, hogy az mekkora erőhatással jár
Egy hullámvasút sem úgy terveződik, hogy minden irányban figyelemben vesszük az 5G-t. 5G túlterhelés és -1G negatív terhelést veszünk figyelembe z-irányban, hosszirányban +/-1,5G és y-irányban (ez lenne kanyarban a centripetális) szintén +/-1,5G. Itt mondhatom, hogy hat 5G pillanatnyilag, mert ez a gravitációs erő síkjába esik és a pálya egyenes. Ha fékezem a kocsikat egy egyenes szakaszon +1,4G-vel, akkor a kocsiszekrényre hat 1,4G x irányban, 0G y irányban és -1G (önsúly) z irányban (egyenes pálya) és 1G negatív (1,4^2+0^2+(-1)^2)^0,5=1,73G terhelés összesen.
Visszatérve az erőkhöz meg a manőverhez. Ballisztikus mozog valami. A beesési szögből kijön egy x irányú gyorsulás (mivel fentről lefelé megyünk), plusz van az 1G gyorsulás z irányban a szabadesésből. Hová kell 20G ennek?