Itt érzek némi zavart az erőben...
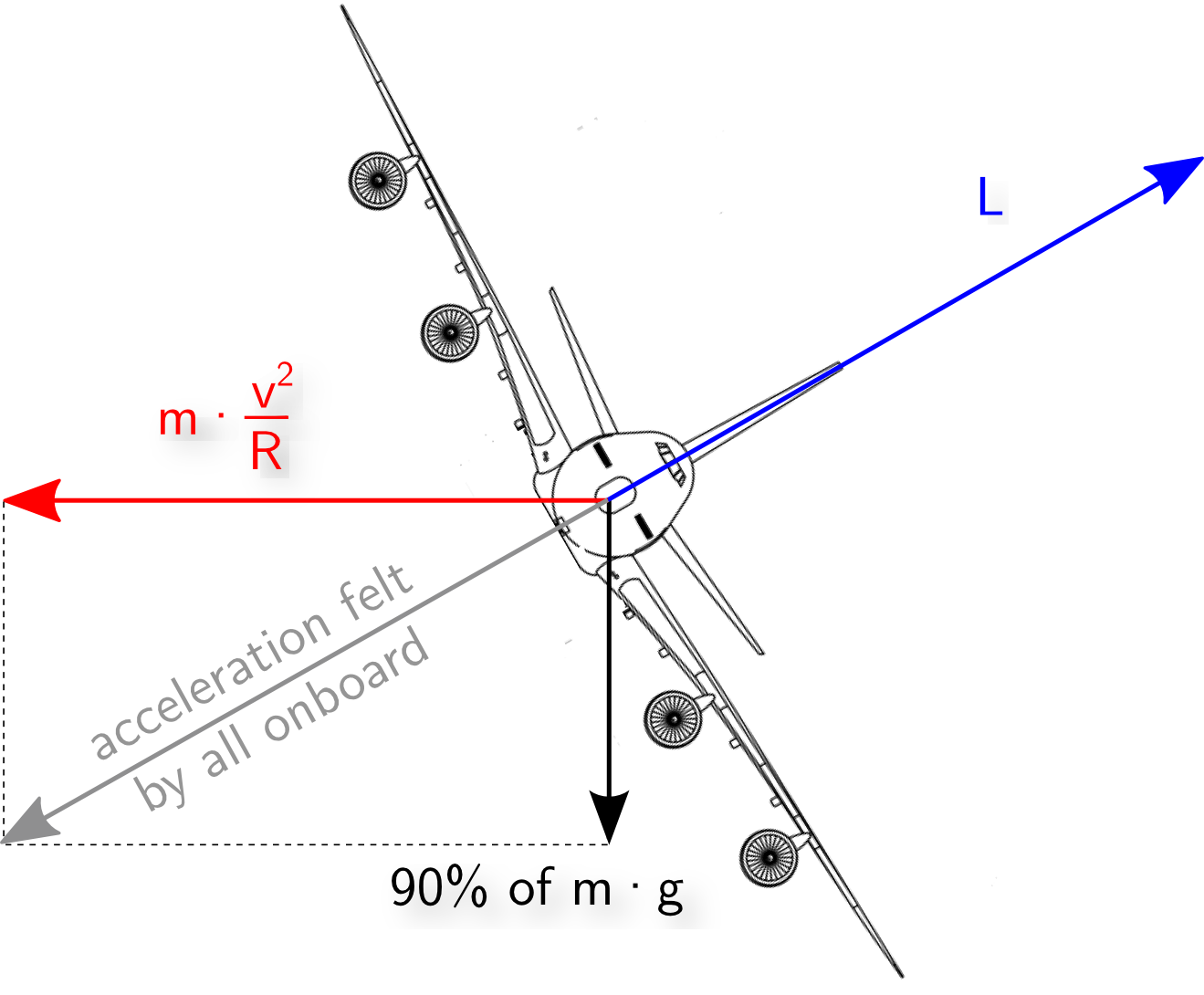
Ez a kép nagyon jó egy pontszerű test esetében, csak a repülőnél ez nem helyes. A repülő egy kiterjedt test, így pontszerű testként modellezve nem tudna repülni, ezért minimum 2d-s kiterjedésű objektumként kell kezelni. Ha így teszünk, akkor fontos lesz a dőlésszöge a hossztengelyhez viszonyítva. Ekkor kell felírni a statikai és kinematikai egyenleteket. Készítettem egy szabadtest ábrát, hogyan is néz ki ez, ha a repülő 2d-s objektum és kanyarodik.
A pontszerű megközelítéssel az a gond, hogy abból indul ki, a tárgy fel van támasztva mondjuk az asztalon. A repülőnél a probléma 2 síkbeli problémává alakul. Egyrészt a gond az, hogy ez statikailag nincs egyensúlyban. Ha az egyensúlyi egyenleteket felírjuk, akkor látható, hogy a feladat
- az x- tengely mentén nincs egyensúlyban. Ahogy bedől a repülő, úgy alakul át az eredetileg felfelé ható felhajtóerőből valamennyi hányad a dőlésszög függvényében x-tengely irányú erővé. Ezzel az erővel viszont semmi sem tart ellen, így ez az erőkomponens gyorsítja a gépet a sugárirányban.
- az y-tengely mentén kvázi egyensúlyi.
(1) Ha a dőlésszög kis mértékű, akkor előáll egy olyan állapot, hogy a felhajtó erő nagyobb, mint a súlyerő, ezért a repülő így emelkedik is és gyorsul sugárirányban - ezt lehet kompenzálni, ha a repülő egyéb aerodinamikai felületeken hoz létre lefelé mutató erőket, így kis dőlésnél sem változik a magasság.
(2) Ha a dőlésszög értéke akkora, hogy felhajtó erő pont akkora lesz, mint a súlyerő, akkor a repülő nem változtatja a magasságát, de a gyorsulás nő.
(3) A harmadik eset, hogy olyan nagy hányada alakul át a felhajtó erőnek a oldalirányú komponensé, hogy a súlyerő már nagyobb, mint a felhajtó erő, így a repülő zuhan az y-síkban, miközben a sugárirányú gyorsulása tovább nő. Ez azt is jelenti, hogy a repülőre ható erők is jelentősen megnőnek.
- a tömeg nem játszik szerepet, ha a (2) eset áll fent, ami az elméleti ideális. Ezért a valóságban az (1) és (3) állapot játszik.



 Hol?Mert ugyanaz a flottakötelék másra képes,ha számithat egy parti bázisra,ahol nagy hatósugarú felderitógépek és szárazfőldi légierő is támogatja a harcát,és másra a nyilt óceán közepén.Plusz ekkor még bejátszik az utánpótlás kérdése is.Merthát a hajóknak üzemanyag is kell,ami mennyisége befolyásolja a manőverlehetőségeiket.
Hol?Mert ugyanaz a flottakötelék másra képes,ha számithat egy parti bázisra,ahol nagy hatósugarú felderitógépek és szárazfőldi légierő is támogatja a harcát,és másra a nyilt óceán közepén.Plusz ekkor még bejátszik az utánpótlás kérdése is.Merthát a hajóknak üzemanyag is kell,ami mennyisége befolyásolja a manőverlehetőségeiket.