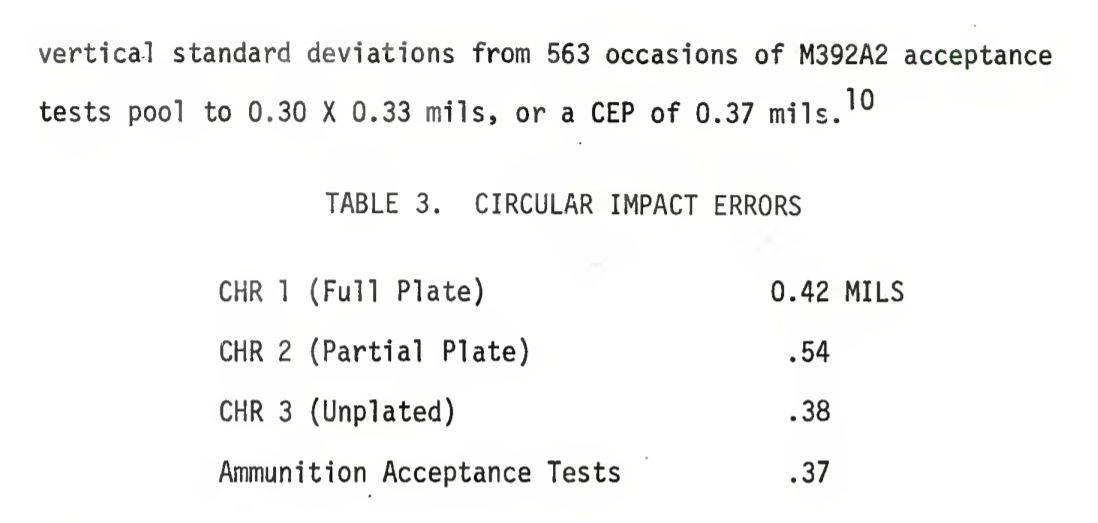
Viszont akkor nézzük meg újra ezt a táblázatot.
Érdekes, hogy totál szimmetrikus a célzási hiba X, Y és a szórás is?
Viszont mivel X,Y koordináta van megadva akkor ezt hogyan kéne értelmezni..?
1500 méteren akkor a +/- 1,2 méter szórás és a kb. 1/3-ad akkora szórásközép hiba ezt jelentené?
Mert akkor egy kb. nagyobb méretű jenki hk ellen is ilyen átfedések mellett ki az, aki szerint 1500 méteren az első találat 50% esélye a rossz egy T-62-vel...?
Mert ebbe a zónába is csak 50%-a esik a találatoknak.
De ezzel az adatsorral se tudok nagyon mit kezdeni, ami egy alapvetően sugárparaméteres rendszernél derékszögű koordináta-rendszert használt .
Én így az ebbe berajzolható kör sugarával számoltam.
A német 2,5x2 méteres lőlapnál is mivel az egyik paraméter kisebb, a másikat kis hibával el lehet dobni és akkor lehet a kettő közti méret sugarát nézni célnak, az eredmény kb. ugyanaz lesz.
Does any of you have any additional reliable data concerning the performance of the individual contenders in the Hellenic Tank Trials ? Any information would be appreciated! Thank you ! This is known: The tanks compared included the M1A2 Abrams, Leopard 2A5, Leclerc, T-80UE and T-84. Of these six...
www.steelbeasts.com
Nézzük már hogy hogyan és mire tüzeltek.
Test 9 : First round hit probability (@1600m; target: 2,3x2,3m still).
Test 10 : Firing on the move on fix target (40km/h; @1000-1200m; target : 2,3x2,3m still; 10 APFSDS).
Test 11 : Evaluation of the precision on still target (still; @2000m; target : 2,3x2,3m still; 10 APFSDS).
Test 12 : Evaluation of the precision of firing on the move on still targets (40km/h; same conditions as before).
Test 13 : Probability of first round hit by night (still; @1000m; target : 2,3x2,3m 1 APFSDS).
Test 14 : Probability of first round hit on the move by night on still target (40km/h; same).
Test 15 : Evaluation of the precision on still targets by night (still; @1500m; target : 2,3x2,3m still; 10 APFSDS).
Test 16 : Evaluation of the precision of firing on the move by night on still targets (40km/h; same).
Test 17 : Probability of first round hit on moving targets (still; @1000m; target : 2,3x4,6m 20-30km/h 1 APFSDS).
Test 18 : Probability of first round hit on the move on moving target (40km/h; @1000-1200m; same).
Test 19 : Evaluation of the precision on moving targets (still; @1500m; target : 2,3x4,6m 20-30km/h; 10 APFSDS).
Test 20 : Evaluation of the precision of firing on the move on still targets (40km/h; @1500-1700m; same).
A moving target esetén tessék csak a cél méretét megnézni. Izé...
Minden lőtáv 1500 méter vagy inkább 1000-1200 méter. Mert itt lehet a tűzvezetés pontosságát kiértékelni.
Miért? Mert a matek a barátunk azért.
Ha fegyver szórása a cél mérete alatt marad, akkor ha azt a célpont közepén vagy számolt találkozási ponton tartod, akkor el fogja találni.
Ha brutálisan alacsonya találati arány, akkor vagy a tűzvezetés vagy a löveg szórása nem igaz vagy egyik sem. És a löveg szórása ami igen jól mérhető és elvileg (dokumentált). Tehát, ha van egy adott pontosságú löveged és folyton mellélő ott, ahol a szórása számottevően a cél mérete alatt van, akkor azt jelenti, hogy a célzás a szar.
A problémám az, hogy CEP értéknek véve 0 hibával a L7A1 táblázatban szereplő értékeket nem jön ki a matek.
Mert azzal nem lesz 17/20 meg ilyen találati arány egy 2,3x2,3 méteres lőlapra sem 1000 méterről sem.
Mert a teljes szóráskép messze a lőlap mérete feletti.
Fogalmazzunk úgy, hogy egyre inkább értelmezési probléma az akkor, hogy mi a szórás.
A legjobb eddig
@Kurfürst szovjet lőlapja, mert az megfelelő koordináta-rendszerben van.
Csak ez az L7A1-hez képest miért ilyen kicsi? Ezt is magyarázza meg már valaki...
2000 méternél ott a 50%-os értéknél 1,6 és 1,6 érték van.
Ez még a négyzetbe rajzolt kör esetén is 160 cm. A 90-nek majdnem duplája...
Ez lenne a fejlődés...?
Egyre nagyobb a zavar.
Használjuk akkor a L7A1 és szovjet D22-őt.
A L7-azt látjuk, hogy lineáris a szórás 500 méterhez képest még 1000, 1500 és 2000 méterig is.
A AAA cikkből látszik, hogy ez addig van, ameddig a lövedék nem lassult le nagyon. Még egy szutyok 23 mm-es lövedéknél is a lineáris tartomány 1000 méterig simán jó modell.
Na, akkor ezzel a D22 2000 méteren 90 cm CEP-je 1000 méteren 45 cm és 1500 méteren a kettő között 67 cm.
A számoló táblázatom R = 1,3 méteres célra:
2000 méternél 35% találati arány
1500 méternél 57% találati arány
1000 méternél 90% találati arány
Na, nézzük ez a TARDOC-hoz.
2000 méternél 25% találati arány
1500 méternél 50% találati arány
1000 méternél 82% találati arány
Ha engem kérdezel az adatok szűkössége, nem a T-62 lövegéről vett adat, de a táblázat modellje és a D22 CEP-jével ennyire pontosan hozza az arányokat. Az eltérés abból ered, hogy nem a löveg pontossága a rendszer pontossága.
A jelleg bizony pontosan az, amit a TARDOC mutat.
@Kurfürst, nincs itt semmiféle "bűzlés".
Csak az átlagember nem érzi jól az arányokat még egyszerűen normál eloszlással sem, nemhogy a kettőssel. Ennyi.
De ezért mérnökök tevezik a dolgokat, akik értik ezeket.

De, ha szerzel T-62 lövegére is értelmezhető adatokat, akkor arra is számolhatok és lehet belőle mini cikk vagy f*szomtudja.
A modellem alapján az L7A1 adatait nem értem. Ha ilyen pontosak lennének a mai lövegek, akkor a görög teszten látható találati arányok nem jöjjének ki. Sokkal kisebb kéne.
Egy biztos. A jenki fickó 5000 méter 50 centibe lövés nettó marhaság. Egész egyszerűen nem értem, hogy mi szülte azt az írást.